教師あり学習を大きく分けると、クラス分類と回帰があります。
前回はPythonでクラス分類器を作成したので、今回は回帰を実装しましょう。
回帰の中でも分かりやすい線形モデルを扱います。イメージ的には以下のような直線を求めることで、未知の入力に対して出力値を予測する感じです!
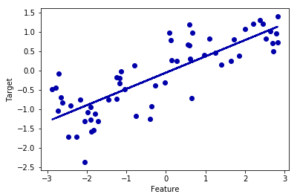
本記事を読めば、線形モデルの回帰をイメージできるようになると共に、様々な回帰手法を扱えるようになると思いますよ。
使用するデータや実行環境については、以前の記事を参照してくださいね。


線形モデルとは
機械学習における線形モデルは、特徴量(入力データ)を線形関数に与えることで未来を予測するものです。
線形モデルの一般的な予測式は以下のようになります。
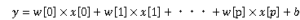
yは予測値、xはデータの特徴量(入力値)、wとbは学習されたモデルのパラメータです。
ちなみに特徴量が1個だと以下のようになります。
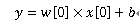
中学校の数学で見たことがありますよね。こいつは傾きw[0]で切片bの直線を表していることが分かります。
線形モデルによる回帰では、入力データから直線を導くことで未来を予測するというイメージで問題ないです。
線形モデルによる回帰の種類
以下のような回帰手法が有名ですが、最も単純な回帰は線形回帰です。
- 線形回帰(最小二乗法)
- リッジ回帰
- Lasso
- エラスティックネット
線形回帰(最小二乗法)を実装しよう!
線形回帰、つまり最小二乗法は最も単純で古典的な回帰手法です。(エクセルでも出来ちゃう。)
流れを超簡単に言うと、以下のように入力データ(青い点)と線との距離を二乗した値の平均が最小となるように線を引くわけです。
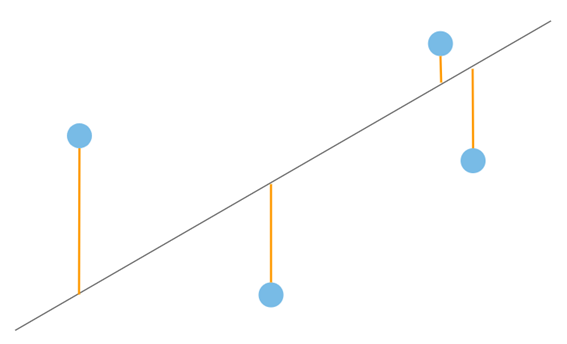
使用するデータ
回帰を始める前に、今回使用するデータを確認・可視化しておきましょう。
確認は結構大事です。
以下のソースコードを打ち込んでshift+enterです!
%matplotlib inline from preamble import * X, y = mglearn.datasets.make_wave(n_samples=60) col=pd.Index(['特徴量(X)'],name='Number') df_x=pd.DataFrame(X,columns=col) df_x['出力値(y)']=y df_x
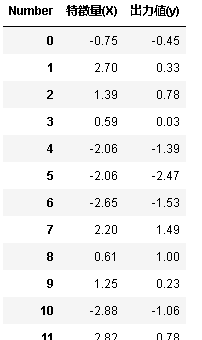
1行目でmatplotlibライブラリ使うぞ宣言してます。
2行目で色んなライブラリをimportするおまじないしてます。ここらへんはいつも通り。
4行目でデータを読み込んでます。Xに入力データ、yに出力データを格納します。都合上mglearnライブラリを使ってますけど、通常はエクセルとかからデータを持ってくると思います。
5行目で表のラベルを作ってます。
6行目でDataFrameメソッド使って表を作ってます。
7行目でyのデータを追加で挿入してます。なんか汚いですねすみません(笑)
8行目で表を出力です。
表を作りたいときは、pandasライブラリを使うと綺麗に作れます。コード中のpdはpandasのpdです。
続いてプロットしてみましょう!
plt.scatter(X,y)
plt.xlabel("Feature")
plt.ylabel("Target")
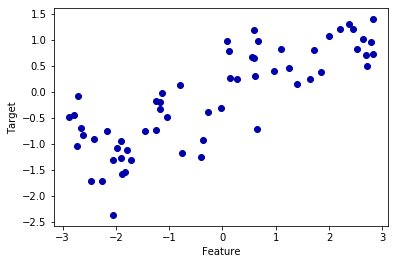
右肩上がりになっているので、ちゃんと予測できそうです。
このようにデータの中身を確認することで、学習・予測する意味があるのかを判別することは大事です。
線形回帰を実装・実行!
それでは実際に回帰を行います。
from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(X, y)
あ、お疲れ様です。学習は終わりました(笑)
前回同様、モデルを作成してfitメソッドで学習してます。
続いて線を予測して表示してみましょう。predictメソッドを使います。
plt.scatter(X,y)
plt.xlabel('Feature')
plt.ylabel('Target')
plt.plot(X, model.predict(X))
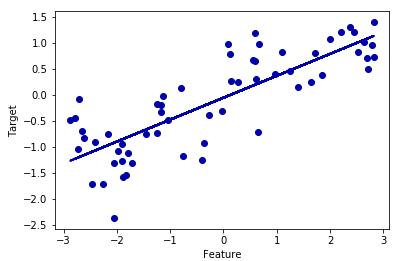
モデルを分析・評価しよう
学習モデルを作成したら、そのモデルの分析・評価は必須です。
まずは、訓練データとテストデータに分けて学習させましょう。
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42) lr = LinearRegression().fit(X_train, y_train)
2行目のようにモデルを作って学習する流れを1行にまとめることもできます。
傾きと切片を確認
print("lr.coef_:", lr.coef_)
print("lr.intercept_:", lr.intercept_)
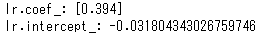
coefが係数 (coefficient) という意味でして傾きwです。
interceptは切片bです。
訓練データとテストデータに対する性能
scoreメソッドを使って性能(スコア)を見ましょう。
print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Test set score: {:.2f}".format(lr.score(X_test, y_test)))
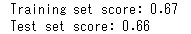
上が訓練データに対するスコア、下がテストデータに対するスコアです。
テストデータに対するスコアが0.66なので精度はあまり高くないですね。
加えて訓練セットとテストセットに対する値が非常に近いので、これはおそらく適合不足であって、過剰適合ではないということです。過剰適合ならテストセットに対する値はもっと下がるはずです。
まとめ
今回は線形回帰を実装・評価しました。
数行でできるから超簡単です。
リッジ回帰やLassoは線形回帰よりも高性能な回帰手法です。
線形回帰と同様に簡単に実装できますので、試してみてはどうでしょうか。
- 線形モデルの回帰による予測線は直線的!
- モデルを作成したら評価も忘れずに。
参考図書
ちなみにこの記事は↓の本を参考にしています。







コメント